题目
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
输入: [1,3,5,6], 5
输出: 2
示例 2:
输入: [1,3,5,6], 2
输出: 1
示例 3:
输入: [1,3,5,6], 7
输出: 4
示例 4:
输入: [1,3,5,6], 0
输出: 0
分析
这道题就是找到数组中的数,遍历就不说了, 我们首先想到的比较好的解法当然是二分搜索
需要注意的是当目标值不存在于数组中时,我们要如何去定位合适的插入点?先上代码再分析。
代码
public int searchInsert(int[] nums, int target) {
return binSearch(0,nums.length-1,target,nums);
}
public int binSearch(int left, int right, int x, int[] nums) {
if (left > right) return left;
int mid = (left + right) / 2;
if (x < nums[mid]) return binSearch(left, mid - 1, x, nums);
if (x > nums[mid]) return binSearch(mid + 1, right, x, nums);
if (x == nums[mid]) return mid;
return -1;
}
这里是采用传统的递归来写二分,但其实这里可以不用,直接一个while循环就行
public int searchInsert(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
// 防止溢出
int mid = left + ((right - left) >> 1);
if (target == nums[mid]) {
return mid;
} else if (target < nums[mid]) {
right = mid - 1;
} else if (target > nums[mid]) {
left = mid + 1;
}
}
return left;
}
二分搜索在目标值大于或小于mid位置的值时要如何改变left和right 就不说了,关键是为什么最后我们把left 作为插入位置呢?
我们可以拿奇数个或偶数个元素的数组试一下,发现如果目标值不在数组中,那么它们最后都会面临这样一种情况:left和right相邻,而目标值就介于两者之间。
举个例子,数组[0,2,4,5,6],目标值3,如下图:
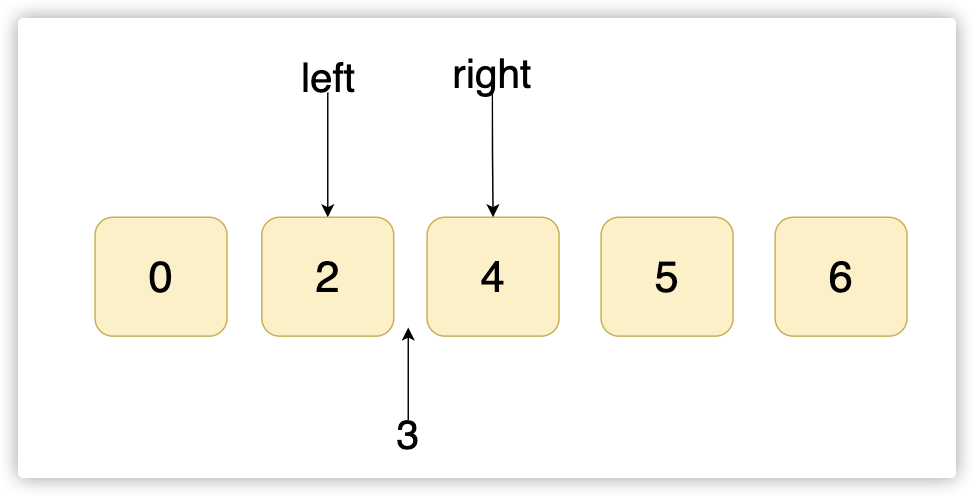
left = mid + 1 ,呈现下面的状态:left和right重叠,且在目标值的大一位
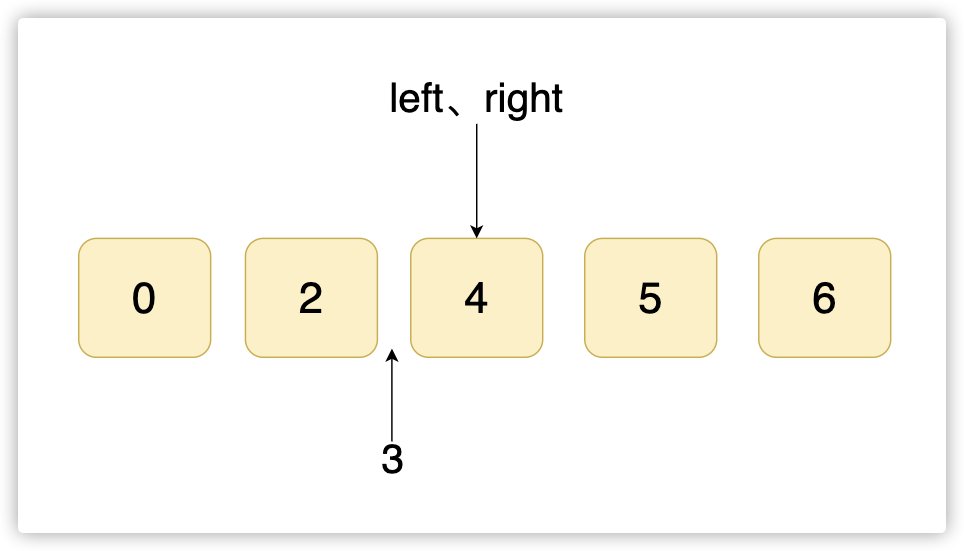
right = mid - 1 ,right左移一位,达到while循环结束条件left>right
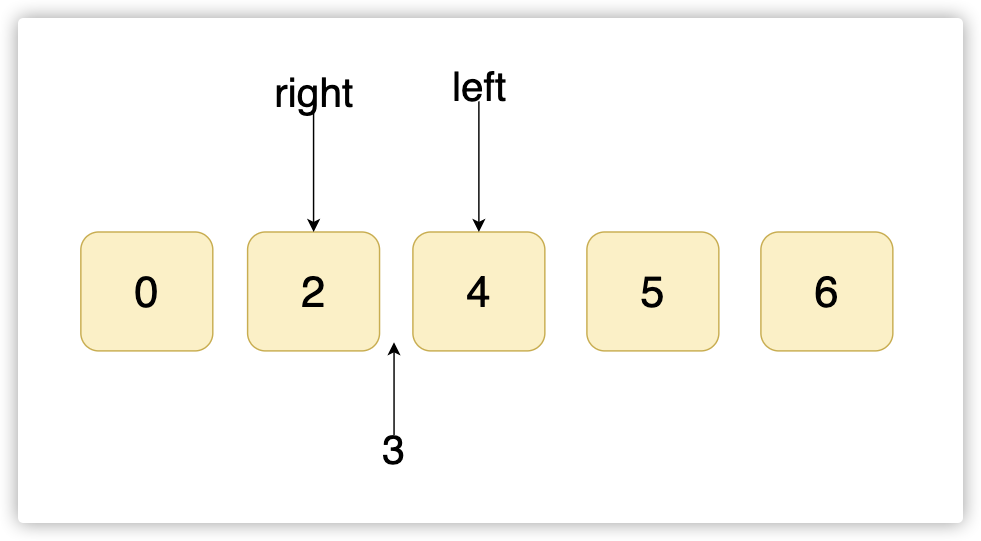
left 作为插入不存在目标值的位置。当然也可以提前一步,当left == right 时那个位置也是一样的,leetcode官方就是这么选择的。
复杂度分析
- 时间复杂度:O(log n),其中 n 为数组的长度。二分查找所需的时间复杂度为 O(log n)。
- 空间复杂度:O(1)。我们只需要常数空间存放若干变量。
这道题主要考察二分搜索,难点在于插入位置的选择。
![Featured image of post [leetcode]35.搜索插入位置](/p/search_insert/leetcode_hua465350402cd0ec3eacd50007e571132_103033_800x0_resize_box_3.png)