红黑树，这次终于拿下了

前言

由于最近在看Java的容器，看到HashMap，发现它底层有用到红黑树，想起了一些段子以及很久之前曾经挑战过学习它但是没有成功，于是这次打算再次挑战一波，并写成博客。

应用场景

JDK的HashMap、TreeMap和TreeSet
Linux内核的虚拟内存管理
epoll监控socket的文件描述符
Nginx的Timer管理
C++的STL

可以看到在实际工程场景中还是用得很多的一种数据结构的。

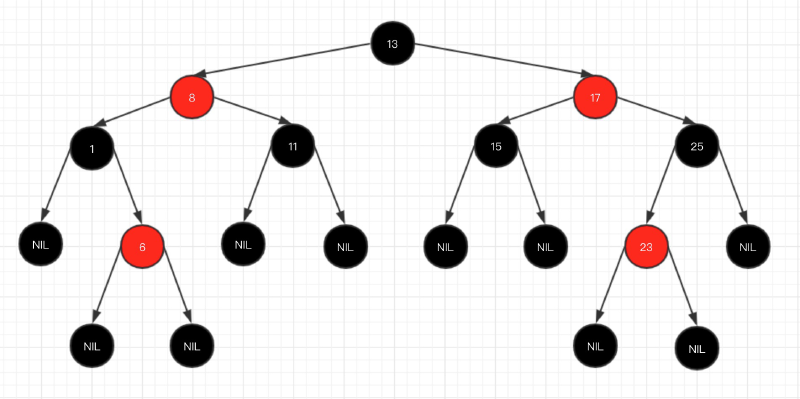
五大基本性质

首先红黑树是一颗二叉搜索树，然后再加上下面五大性质：

节点有红色和黑色两种
根节点一定是黑色的
叶子节点（nil节点）都是黑色的
不能有连续的红色节点
任意节点到叶子节点所经过的黑色节点数相同

第5点就是红黑树维持平衡的重要条件，我们常说的达到黑色平衡或者红黑树达到平衡主要说的就是达到这个条件。

如果精力充足的话建议可以再去了解一下2-3-4树，红黑树就是对概念模型2-3-4树的一种实现，这里推荐我当时看的敖丙写的一篇文章，介绍了2-3-4树的概念及其与红黑树的转化，最后介绍了红黑树的简化版——左倾红黑树的插入与删除。

本质与意义

这一部分要说的就是面试经常问的：为什么有了二查找查找树/平衡树还需要红黑树？

二叉查找树的缺点

二叉查找树大家应该很熟悉，特点就是左子树的节点都比父节点小，而右子树的节点值都比父节点大。基于这个特点，我们在二叉查找树查找某一个值时，采用类似二分查找的思想，时间复杂度只用O(logn)。

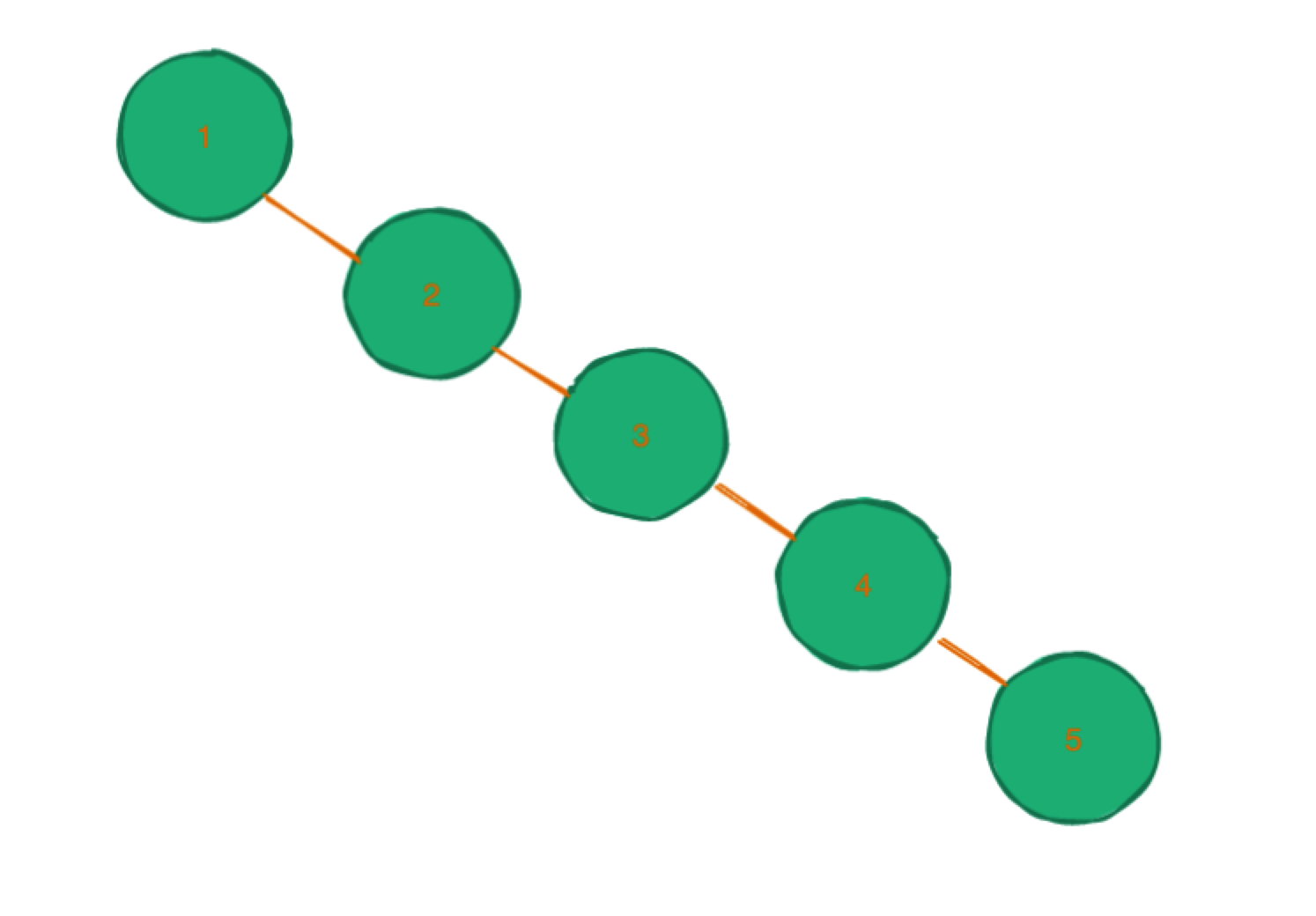
但是这是正常情况下，因为二叉查找树有可能出现一种极端，就是所有节点都同一方向上（如下图），这个时候二叉搜索树以及近似退化为一条链表了，查找的时间复杂度也顿时变成了O(n) ，那这样的话二叉搜索树也就失去了原本的意义——让搜索变得更快。

为了解决这个问题，出现了平衡二叉搜索树（也就是我们常说的AVL树）。

AVL树

为了解决二叉搜索树可能退化为链表的问题而生，有以下特点：

拥有二叉搜索树的全部特性
每个节点的左子树和右子树的高度差不超过1

由于第二点的约束使得AVL树不会出现大量节点一边倒的情况，但是在AVL树构建的过程中就需要很多额外的操作来保证其符合这个特性，使得其最坏情况下查找的时间复杂度也还是为O(logn)

为什么有了AVL树还要红黑树？

虽然AVL树解决了二叉搜索树退化了近似链表的缺点，但是由于每个节点的左子树和右子树的高度差不超过1这个要求实在是太严苛了，导致每次插入和删除节点的时候很容易就破坏了这条规则，之后就需要左大量的左旋和右旋来进行调整时期再次符合AVL树的要求。

所以如果在插入和删除很频繁的场景中，AVL树需要很频繁地进行调整，这样的话效率就大大降低了，为了解决这个问题所以出现了红黑树。（如果在面试中接下来这里就可以说出红黑树的那5个特点）。

正由于红黑树的这些特点，使其最坏情况下不仅还能维持用O(logn)的时间复杂度找到某个节点，而且与AVL树相比，优势就在于不会那么频繁地破坏红黑树的规则，从而不用那么频繁地进行调整，这就是我们大多数情况下使用红黑树的原因。

所以红黑树是一种相对AVL树来说不那么严格的平衡树，也就是一种折中的方案，介于普通的二叉搜索树和AVL树之间。极端情况下左右子树的节点数（也就是深度）相差一倍，也就是左边都是黑节点，右边都是红黑相间，右子树的节点数或者说深度就也是左子树的2倍，这个要求就比AVL树的相差最多只能为1宽松多了，因此调整也就更少，效率也就更高。

为什么红黑树查找的时间复杂度还能维持在O(logn)？

我们对最坏情况下的时间复杂度进行计算。

最坏情况下就是上面说的红黑相间，总节点数=红节点数+黑节点数，红黑节点数一致。

$$n = n_r + n_b$$

所以时间复杂度就是

$$O(2* \log n_b ) = O(2 * \log \frac{n}{2})$$

常数2直接去掉

$$O(\log \frac{n}{2}) = O(\log n - 1)$$

然后因为这里是二分，所以log底数取2，就转换为如上的最终形式，去掉常数-1后可以发现此时最坏情况下的时间复杂度仍然还是O(logn) 。

红黑树的插入

下面要介绍的插入和删除操作涉及左旋和右旋概念，需要先保证了解这两个基本操作。

插入和删除操作推荐用这个数据结构动画演示网站搭配食用：https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

总结表格

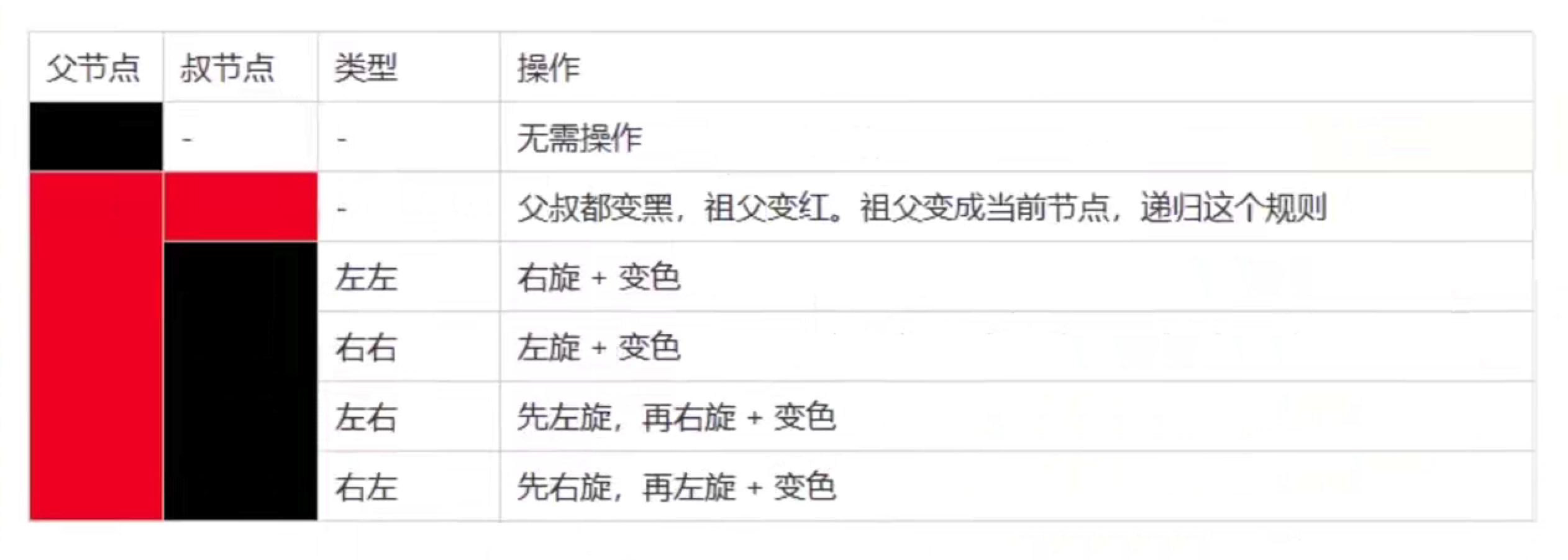
插入操作的话相对删除还是要简单一点的，但是还是分出了几种情况，这里就用b站up free-coder总结的表格：

叔节点：父节点的兄弟节点

祖父节点：父节点和叔节点的父节点，也就是爷爷节点

为了尽可能不去破环平衡，我们插入的新节点都是默认为红色的，插入后再检查是否破坏了红黑树的定义，如果破坏了我们再去进行调整。

具体解析

表格中一共有6种情况，由于其中有两组是镜像的，所以下面归纳为4中情况：

情况1：父节点是黑节点

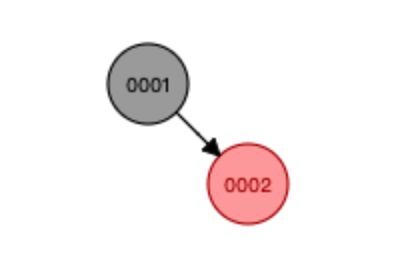
由于父节点是黑节点，插入的新节点就一定是红节点（因为不能有连续的红节点），而红节点不影响红黑树的平衡，所以也无需任何调整操作了。

如图，父节点是根节点也就是黑的，值为1，插入了一个2为红节点，所以无需任何操作。

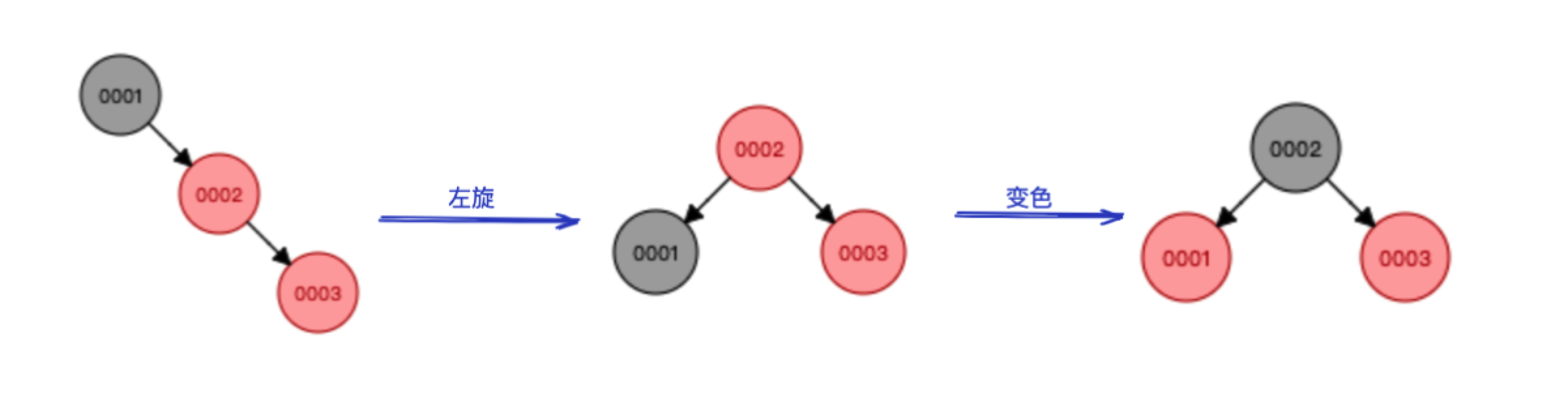
情况2：父节点是红节点，叔节点是黑节点（“左左”和“右右”类型）

在情况1的基础上我们插入一个3

可以看到此时3的父节点2是红，叔节点nil节点是黑的，我们先进行一个左旋，发现出现连续的红色，所以再进行一个变色即可。

这里2和3节点都是它们各自父节点的右子节点，也就是对应上面表格中类型的“右右”，但其实“左左”只是镜像了一下，这里就不再赘述。

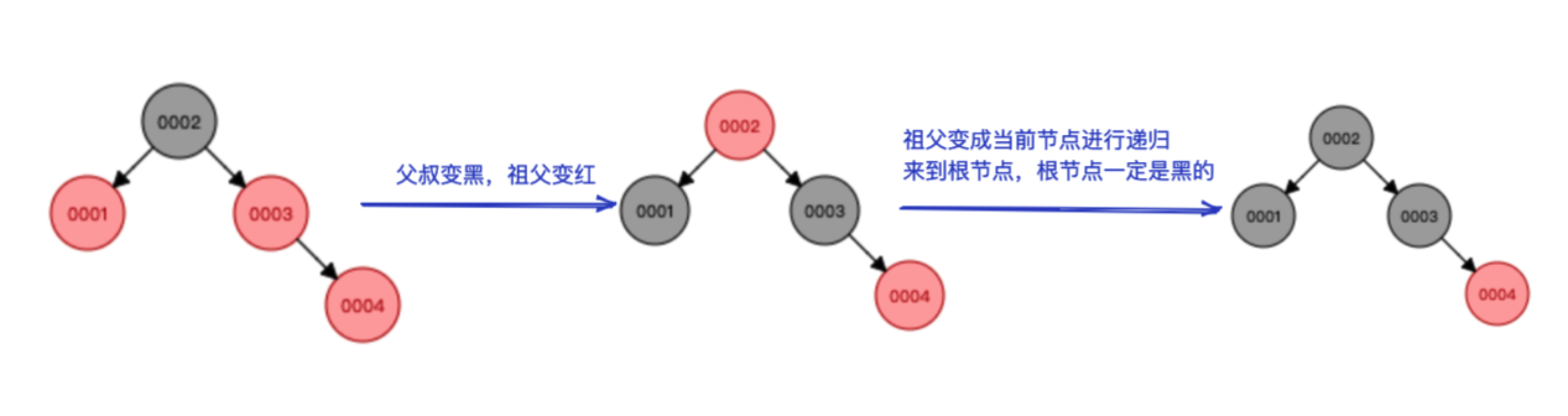
情况3：父节点和叔节点都是红

我们在情况2 的基础上再插入一个4

插入4后父亲节点3和叔节点1都是红的，所以我们把父叔都变黑，祖父变红，然后祖父变为当前节点，向上递归这个逻辑直到根节点，由于根节点一定是黑的所以就把节点2变黑即可。

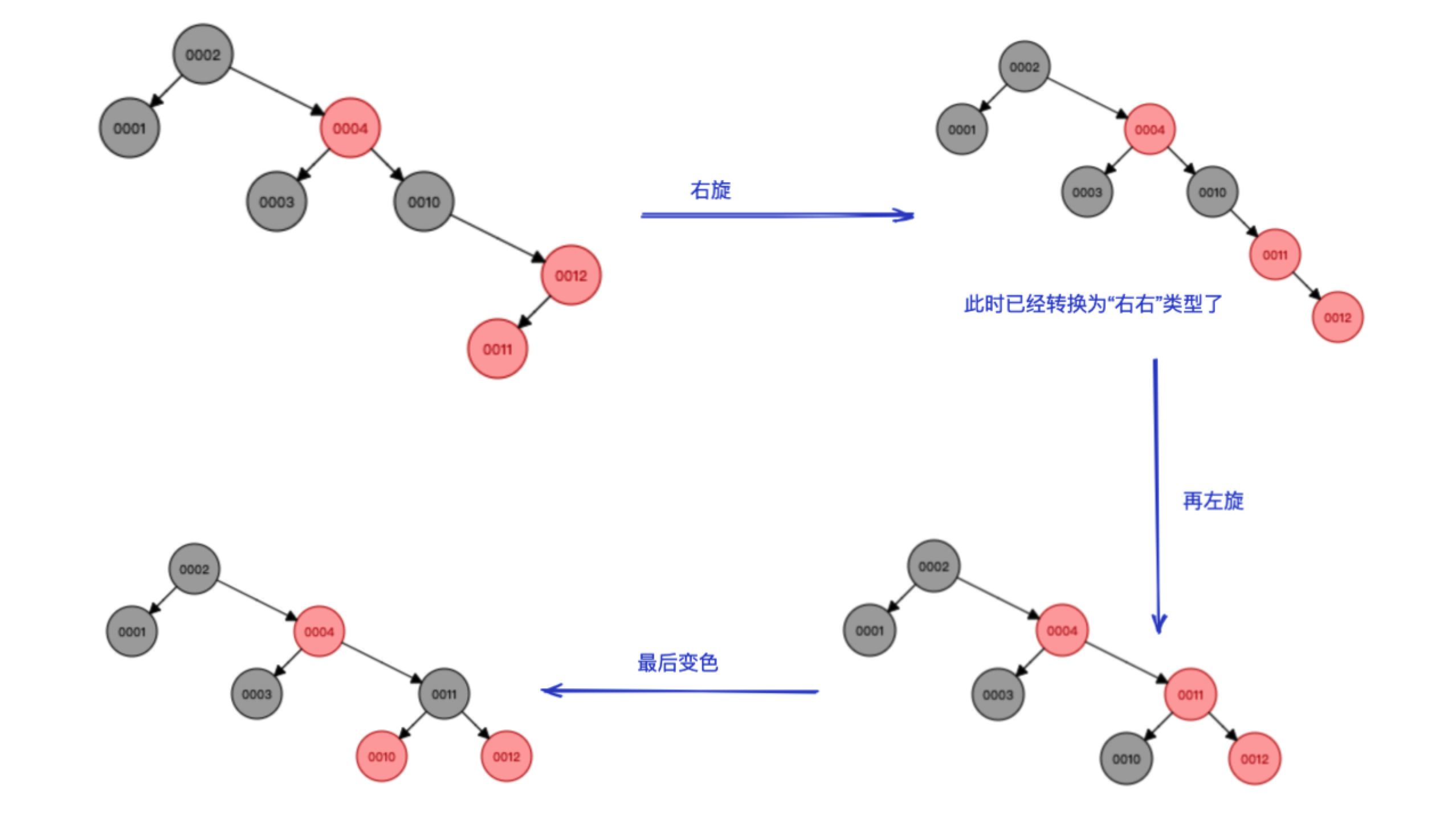
情况4：父节点是红节点，叔节点是黑节点（“左右”和“右左”类型）

这里插入的是11，我们发现插入11后，节点10、12、11形成了一个“右左”类型，形状上就是一个折了一下的类似三角的感觉，这时我们只需要右旋一下，诶就转为“右右”类型了，然后再按“右右”类型去左旋+变色就可以调整完成。

同样的，“左右”类型和“右左”类型是镜像，这里也不再赘述。

红黑树的删除

删除操作是红黑树中最难、情况最多的操作。红黑树的其他方面我感觉还行，就是删除操作我感觉才是红黑树难的精髓之处。

通过替换来删除

删除和插入一样，都可能会破坏红黑树原本的性质，所以在删除后我们是需要做一些调整才让树维持红黑树的性质。

首先从我们直觉上来看，如果删除的节点位于叶子节点处，或者相对来说位置比较低，那删除节点后应该对整棵树的影响会比较小，所需做的调整应该也简单很多甚至不用调整。但是如果被删除的节点位于树的相对中间的位置，而且这个节点还有左右子树，那要做的调整相对来说就会多一点。

所以，我们一般采用一种方法，就是通过替换去删除，具体来说就是找到被删除节点的左邻节点或者右邻节点，然后把左邻或右邻节点放到被删除节点进行覆盖，然后把左邻右邻节点原来位置上的节点进行删除。

左邻和右邻是我自己叫的名字，实际上就是在这棵搜索树的所有节点中，排序刚好比被删除节点小一位和大一位的节点，具体在位置：

左邻节点：本节点左子树中的最大节点，即左子树中最右的节点

右邻节点：本节点右子树中的最小节点，即右子树中最左的节点

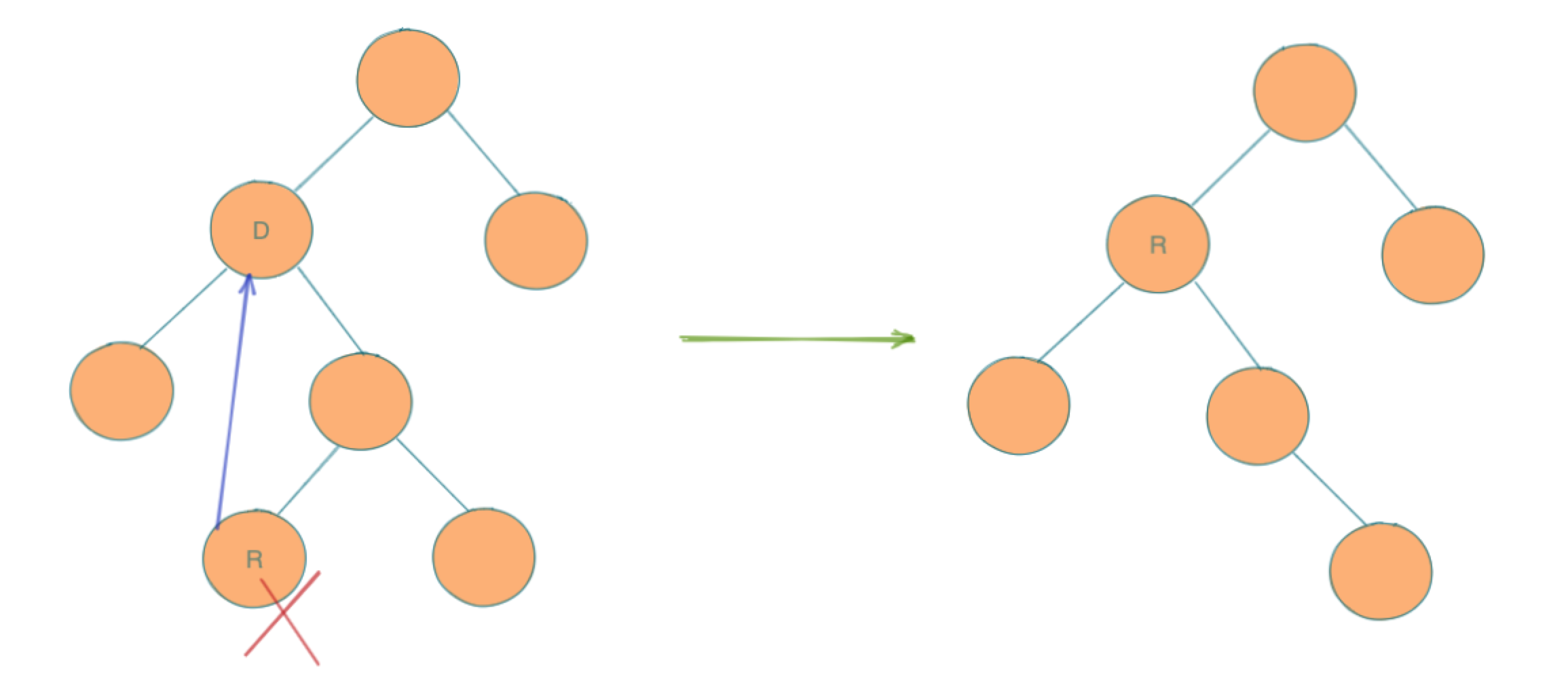
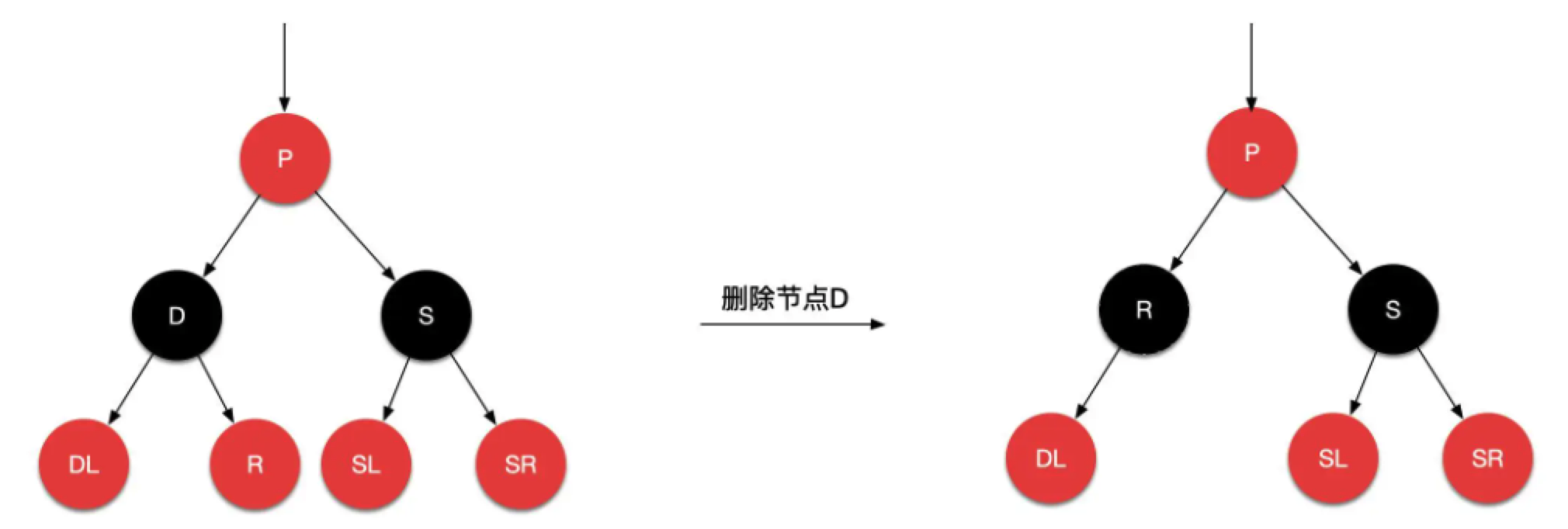
示例：

如图，D是被删除节点，R是其右邻节点，我们用R覆盖了D，然后把R原来位置删除，就完成了这个过程。

然后我们将删除分为三种情况：

情况一：被删除节点无子节点，直接删除
情况二：被删除节点只有一个子节点，用子节点替换要被删除的节点
情况三：被删除节点有两个子节点，可以用左邻节点或者右邻节点进行替换删除操作

所以实际上三种情况都可以概括为这样一个过程：找到一个用来替换的节点，覆盖要被删除的节点，最后再删除用于替换的节点原本所在的节点。

具体到红黑树，可以分为三大场景，9种小情况，其中场景二和三互为镜像，可以结合在一起看。

删除场景一

删除场景一：替换节点是红节点

替换节点如果是红节点，删除之后不影响红黑树的平衡，只需要把让替换节点覆盖后把颜色设置为被删除节点原来的颜色即可。

删除场景二

删除场景二：替换节点是黑色节点，而且此替换节点是它父节点的左子节点

由于替换节点是黑色节点，删除后势必会破坏红黑树的黑色平衡，所以要进行调整，这里又分出四种小情况。

情况2.1：替换节点的兄弟节点是红节点。

删除替换节点（黑）后，左子树的黑色节点会减少一个，所以我们要进行的操作是用替换节点的兄弟节点来补充一下左子树的黑节点数。

具体操作：将替换节点的父节点P设为红色，兄弟节点S设置为黑色，然后对节点P左旋操作，转换为情况2.4 ，接下来就用情况2.4 的操作继续进行。

注意场景二、三的图例都是还没进行覆盖和删除的时候的R，只是根据其位置和周边节点的特点来讨论和推断它被删除后红黑树平衡被破坏的状态以及之后要采取的自平衡操作。

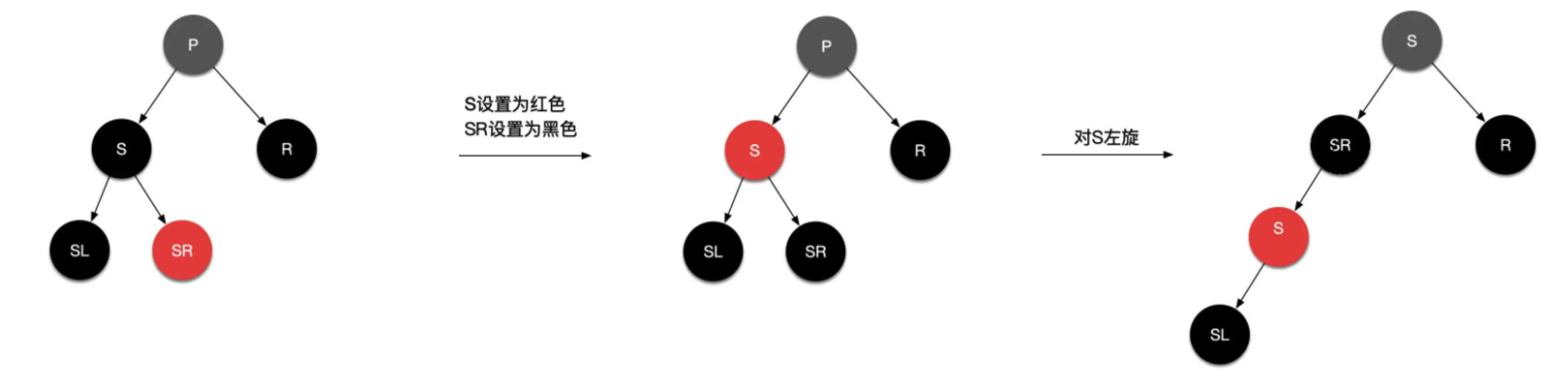
情况2.2：替换节点的兄弟节点是黑色，同时兄弟节点的右子节点是红色的，左子节点任意颜色

这种情况同样要借助兄弟节点来补充左子树的黑节点数，达到平衡。

注意图中的灰色节点表示可以为任意颜色

具体操作：将替换节点的兄弟节点S设置为父节点的颜色，兄弟节点的右子节点SR设置为黑色，父节点P设置为黑色，然后对P进行左旋操作。此时发现同样也是给左子树补了一个黑节点同时右子树黑节点数不变。

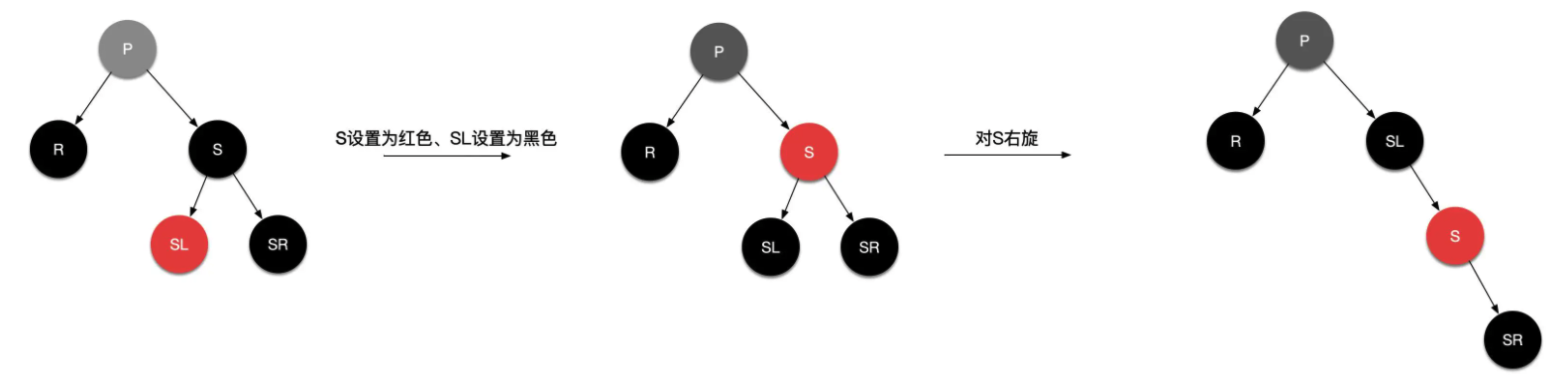
情况2.3：替换节点的兄弟节点是黑色，且兄弟节点的左子节点是红色，右子节点是黑色

具体操作 ：将兄弟节点S设置为红色，兄弟节点的左子节点SL设置为黑色，再对节点S进行右旋，这时候就转换为情况2.2了，按2.2的步骤继续操作即可。

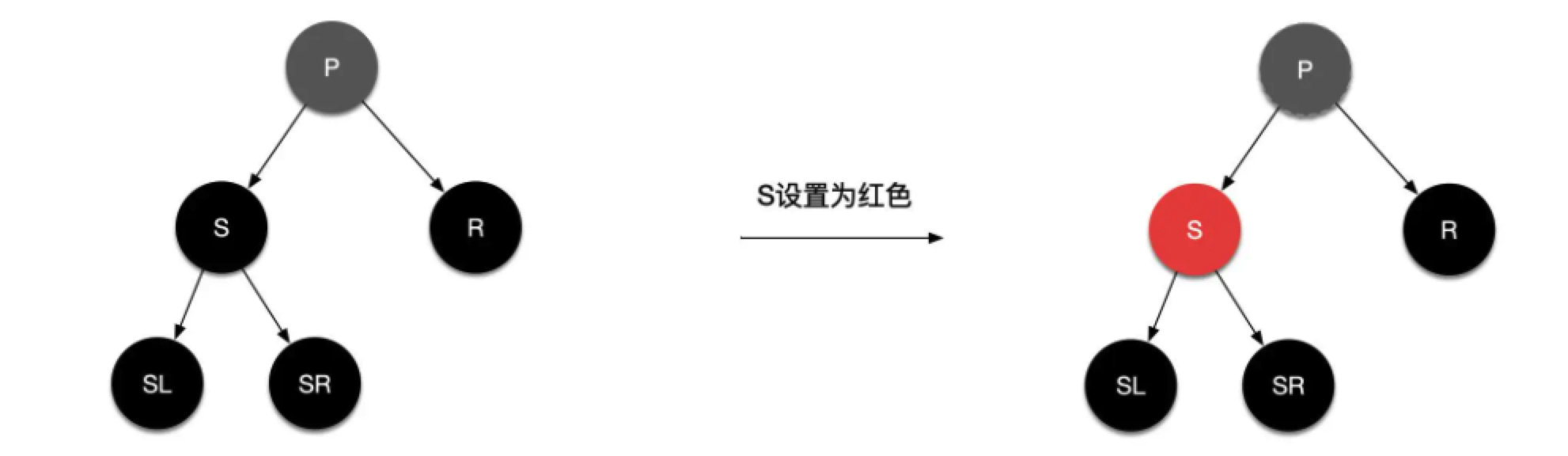
情况2.4：替换节点的兄弟节点的左右子节点都是黑色

具体操作 ：把替换节点当作当前节点，当前节点的兄弟节点S设为红色，然后把父节点P当作当前节点（相当于向上移动当前节点的指针），然后自底向上递归处理。

可以看到，局部上就把右子树的黑节点数减少了1，达到平衡，可是把S变为红色之后有可能破坏红黑树不能有连续的红节点的规则，所以还需要递归向上处理。

删除场景三

删除场景三：替换节点是黑色节点，而且此替换节点是它父节点的右子节点

场景三就是场景二的镜像了，所以场景二是左子树少了一个黑节点数需要补，场景三是右子树少了一个黑节点数需要补。看场景三建议结合场景二一起看，这一部分就相对写得简略一点了。

情况3.1：替换节点的兄弟节点是红节点

具体操作：将替换节点的父节点P设置红色，将兄弟节点S设置成黑色，再对节点P右旋操作，转换为情况3.4。

情况3.2 ：替换节点的兄弟节点是黑色，且兄弟节点的左子节点是红色、右子节点是任意颜色

具体操作：替换节点的兄弟节点S设置成父节点P的颜色，兄弟节点的左子节点SL设置为黑色，父节点P设置为黑色，再对节点P右旋操作。

相当于给右子树补充了一个黑节点。

情况3.3 ：替换节点的兄弟节点是黑色且兄弟节点的右子节点是红色、左子节点为黑色

具体操作：替换节点的兄弟节点S设置成红色，兄弟节点的右子节点SL设置为黑色，再对节点S左旋操作，转换到了情况3.2，再进行情况3.2的操作。

情况3.4：替换节点的兄弟节点的左右子节点都是黑色

具体操作：把替换节点当作当前节点，当前节点的兄弟节点S设为红色，然后把父节点P当作当前节点（相当于向上移动当前节点的指针），然后自底向上递归处理。

写在最后

经过一天多高强度看文章以及视频，算是学得七七八八了。虽然面试不太会经常问到红黑树而且尽管问到一般也不会深入到具体的插入和删除过程，最多性质和意义就得了，所以很多人都说如果面试官让你手写红黑树那证明他不想要你，你就可以直接告辞了😂 。但是我觉得在实际工程中使用这么广泛的数据结构作为一个程序员还是要好好学一下的，所以才肝出了这篇文章。

所以很多时候为了功利很多知识的学习只是为了应对面试，就比如八股文的学习，但是作为一个程序员这样的身份，还是要有那股我们一直以来最崇尚的求知欲，尽管是八股文的学习，也要学得明白、学得透彻才行。