[leetcode]209.长度最小的子数组

题目

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1:
输入: target = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的子数组.

示例 2:
输入: target = 4, nums = [1,4,4]
输出: 1

示例 3: 
输入: target = 11, nums = [1,1,1,1,1,1,1,1]
输出: 0

提示：

1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105

分析

这道题一开始想到的是暴力解法，也就是把每种可能的子数组长度都试一遍，后来发现这是道典型的滑动窗口题目，用滑动窗口就解决了。之后看官方题解有前缀+二分搜索的方法作为扩展。

代码

滑动窗口

public int minSubArrayLen(int target, int[] nums) {

    if (nums.length == 0) {
        return 0;
    }

    int left = 0, right = 0;
    int s = nums[0];
    int windowLen = Integer.MAX_VALUE;

    while (right < nums.length - 1) {
				// 右指针移动
        while (s < target && right < nums.length - 1) {
            right++;
            s += nums[right];
        }
				// 左指针移动
        while (s >= target) {
            windowLen = Math.min(windowLen, right - left + 1);
            s -= nums[left];
            left++;
        }
    }
    return windowLen == Integer.MAX_VALUE ? 0 : windowLen;
}

方法很简单，就是一个左指针，一个右指针，窗口的范围就是2个指针之间的元素。

一开始先移动右指针直到窗口内和大于等于target

然后向右开始移动左指针，直到窗口内和小于target，由于每次就是一次满足s≥target的窗口，我们就要每次和当前的窗口长度进行比较从而找到最小的窗口长度，也就是最小的子数组长度。

如果窗口长度为最大的int值说明没有找到任何一个满足s≥target的窗口，返回0。

复杂度分析

时间复杂度：O(n)，其中 n 是数组的长度。指针最多各移动n次。

空间复杂度：O(1)。

前缀+二分搜索

public int minSubArrayLen(int target, int[] nums) {

    int n = nums.length;
    if (n == 0) {
        return 0;
    }
    int windowLen = Integer.MAX_VALUE;
    int[] sums = new int[n + 1];
    // 前i个数之和
    for (int i = 1; i <= n; i++) {
        sums[i] = sums[i - 1] + nums[i - 1];
    }
    for (int i = 0; i < n; i++) {
        int s = target + sums[i];
        // 二分搜索
        int bound = Arrays.binarySearch(sums, s);
        // bound为负数表示找不到，返回的是插入位置，且从1开始
        if (bound < 0) {
            bound = -bound - 1;
        }
        // 找到最小的
        if (bound <= n) {
            windowLen = Math.min(windowLen, bound - i);
        }
    }
    return windowLen == Integer.MAX_VALUE ? 0 : windowLen;
}

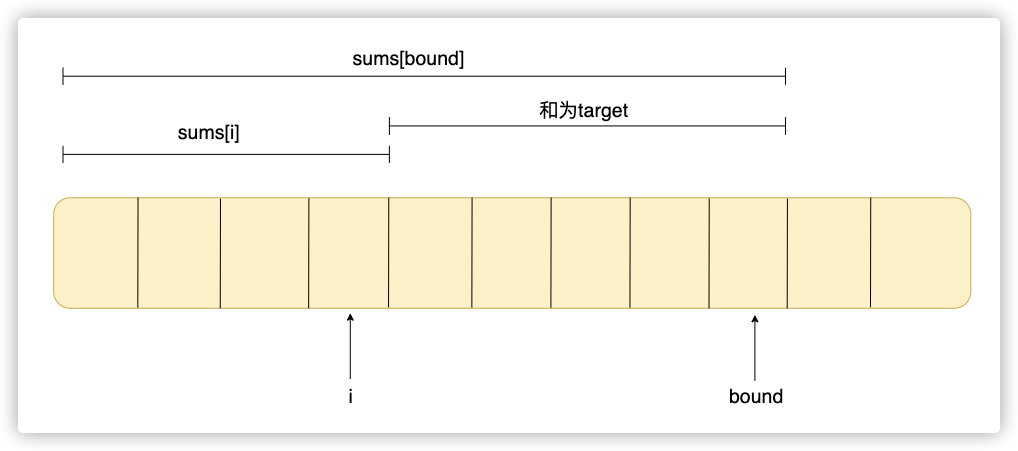
这个方法我们先计算出nums中不同长度的前i个数之和的数组sums，也就是sums[i]表示nums[0]到nums[i-1]中的所有数之和。

然后我们用二分查找在sums数组中找到下标bound，使得sums[bound]-sums[i]>=target，且这个bound是所能找到的最小的。（由于nums都是正整数，sums一定是递增的，所以可以用二分搜索）

最终bound-i就是我们要找的最小的窗口长度。

这里的二分搜索如果找不到的话要返回插入的位置，Java有个Arrays.binarySearch()工具类可以使用，返回值为：

如果找到关键字，则返回值为关键字在数组中的位置索引，且索引从0开始
如果没有找到关键字，返回值为负的插入点值，所谓插入点值就是第一个比关键字大的元素在数组中的位置索引，而且这个位置索引从1开始。

贴个这个工具类的源码：

private static int binarySearch0(long[] a, int fromIndex, int toIndex,
                                   long key) {
    int low = fromIndex;
    int high = toIndex - 1;

    while (low <= high) {
        int mid = (low + high) >>> 1;
        long midVal = a[mid];

        if (midVal < key)
            low = mid + 1;
        else if (midVal > key)
            high = mid - 1;
        else
            return mid; // key found
    }
    return -(low + 1);  // key not found.
}

复杂度分析

时间复杂度：O(nlogn)，其中n是数组的长度。需要遍历每个下标作为子数组的开始下标，遍历的时间复杂度是 O(n)，对于每个开始下标，需要通过二分查找得到长度最小的子数组，二分查找得时间复杂度是 O(logn)，因此总时间复杂度是 O(nlogn)。
空间复杂度：O(n)，其中 n 是数组的长度。额外创建数组 sums 存储前缀和。