[leetcode]59.螺旋矩阵II

题目

给你一个正整数 n ，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例1:
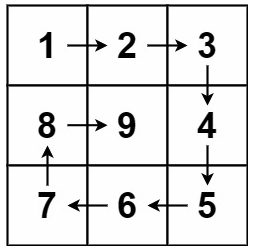
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]

示例2:
输入: n = 1
输出: [[1]]

分析

第一次看到这道题感觉很懵很难，其实这道题也不涉及什么经典算法，就是考验你用代码复现这个过程道能力。

我们可以把按照题目给的图的按顺序去填充矩阵中的值，从第一个位置开始先从左到右➡️ ，再从上到下⬇️ ，再从右到左⬅️ ，再从下到上⬆️ 。如此循环，直到填充完毕，当然如果n为奇数的话就要考虑中间那一格需要最后去单独填充，偶数的话就没有这个问题。

当然每次循环还需要注意，每行/列都遵循的是左闭右开的原则，也就是说从头填到倒数第二个，最后一个就是下一行/列的，才能保证行/列填充行为的统一性。

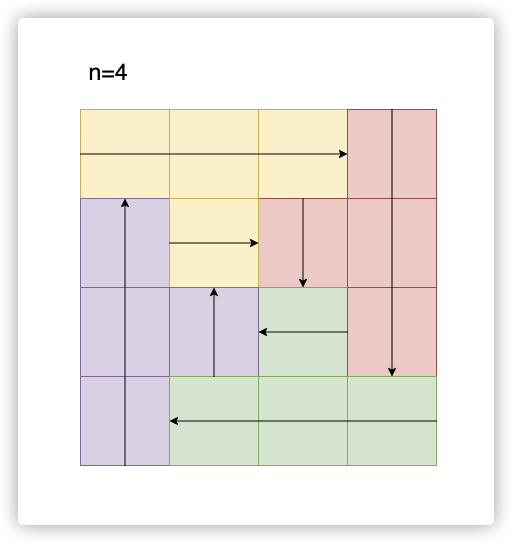
还有一点是每次循环之后，每行/列需要填充的个数就要少2，看下下面的图就可以很直观的理解了。

下面就是n=5和n=4的例子：

代码

class Solution {
    public int[][] generateMatrix(int n) {
        // 矩阵本体
        int[][] matrix = new int[n][n];
        // 横行和纵向开始填充的起始点
        int startx = 0, starty = 0;
        // 循环次数
        int loop = n / 2;
        // n为奇数时矩阵的中间格
        int mid = n / 2;
        // 用来填充的数字，从1开始
        int count = 1;
        // 每列或每行在循环一次后，下一次循环时要填充的元素个数会减少2，用这个变量来记录当前减少的大小
        int offset = 1;
        // 填充时用的指针，i为行，j为列
        int i, j;

        while (loop-- != 0) {
            // 指针置于起始位置
            i = startx;
            j = starty;

            // 上行，从左到右
            for (j = starty; j < starty + n - offset; j++) {
                matrix[i][j] = count++;
            }

            // 右列，从上到下
            for (i = startx; i < startx + n - offset; i++) {
                matrix[i][j] = count++;
            }

            // 下行，从右到左
            for (; j > starty; j--) {
                matrix[i][j] = count++;
            }

            // 左列，从下到上
            for (; i > startx; i--) {
                matrix[i][j] = count++;
            }

            // 循环一次后，下一次起始位置+1
            startx++;
            starty++;
            // 下一次循环时，每行/列填充的个数要-2
            offset += 2;
        }

        // n为奇数要填中间一格
        if (n % 2 == 1) {
            matrix[mid][mid] = count;
        }

        return matrix;
    }
}

复杂度分析

时间复杂度：O(n^2)，其中 nn 是给定的正整数。矩阵的大小是 n \times nn×n，需要填入矩阵中的每个元素。
空间复杂度：O(1)。除了返回的矩阵以外，空间复杂度是常数。